Dall'equazione generale di una conica alle forme canoniche
Aggregazione dei criteri
metodo del completamento del quadrato
Con \( A \cdot C \neq 0 \) e \( A \neq C \) l'equazione rappresenta un'ellisse o un'iperbole con gli assi di simmetria paralleli o coincidenti con gli assi cartesiani.
Infatti è possibile applicare il metodo del completamento del quadrato e scrivere l'equazione nella forma:
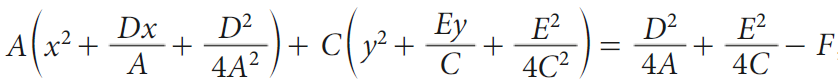
da cui se poniamo 
otteniamo:
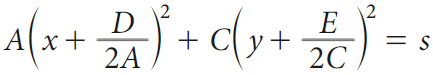
Se consideriamo la traslazione di vettore 
otteniamo l'equazione in forma canonica della conica:
Poiché operiamo una traslazione, la curva che otteniamo è congruente a quella di partenza e dal suo studio possiamo quindi ricavare che tipo di conica è quella iniziale. Il centro di simmetria della conica coincide con l’origine degli assi.
Distinguiamo due casi:
