Sezioni coniche

Data una retta r nello spazio che intersechi in V la retta a, si chiama superficie conica a due falde la superficie generata in una rotazione completa di r attorno ad a.

La parte di spazio racchiusa dalla superficie è detta cono a due falde. La retta r, e ogni altra retta r' della superficie conica, si dice generatrice. L'angolo \( \theta \) che r forma con a si chiama semiapertura. L'asse di rotazione è anche asse di simmetria del cono. V è detto vertice del cono.

La parabola, la circonferenza, l’ellisse e l'iperbole sono dette anche sezioni coniche o semplicemente coniche proprio perché tali curve si possono ottenere sezionando con un piano, non passante per il vertice, una superficie conica a due falde.

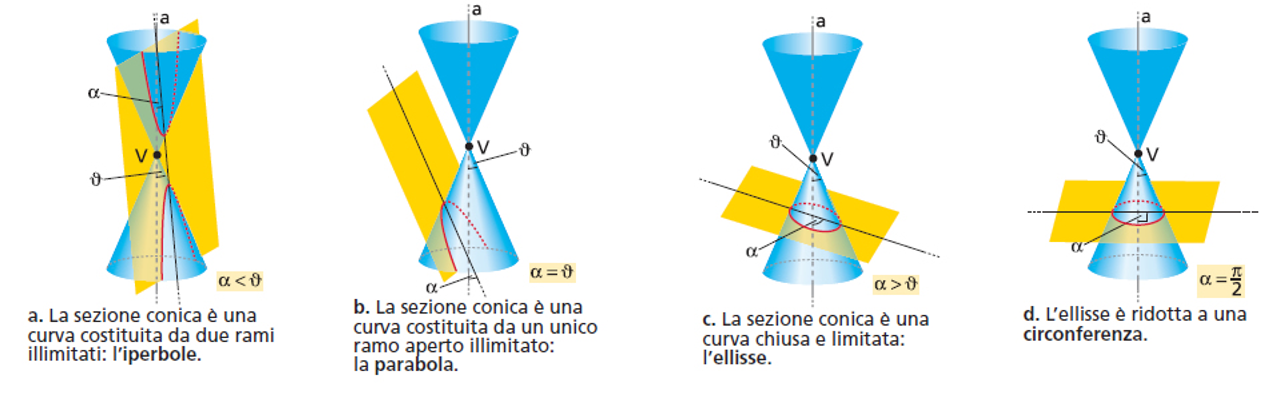
Al variare dell’inclinazione del piano rispetto al cono si ottiene:

1. un'iperbole se l’angolo \( \alpha \) formato dal piano secante con l’asse del cono è minore dell'angolo di semiapertura \( \theta \) del cono
2. una parabola se l’angolo \( \alpha \) formato dal piano secante con l’asse del cono è uguale alla semiapertura \( \theta \)
3. un'ellisse se l’angolo \( \alpha \) formato dal piano secante con l’asse del cono è maggiore della semiapertura \( \theta \).
   Se, in particolare,  \( \alpha = \frac{ \pi }{2} \), abbiamo una circonferenza.

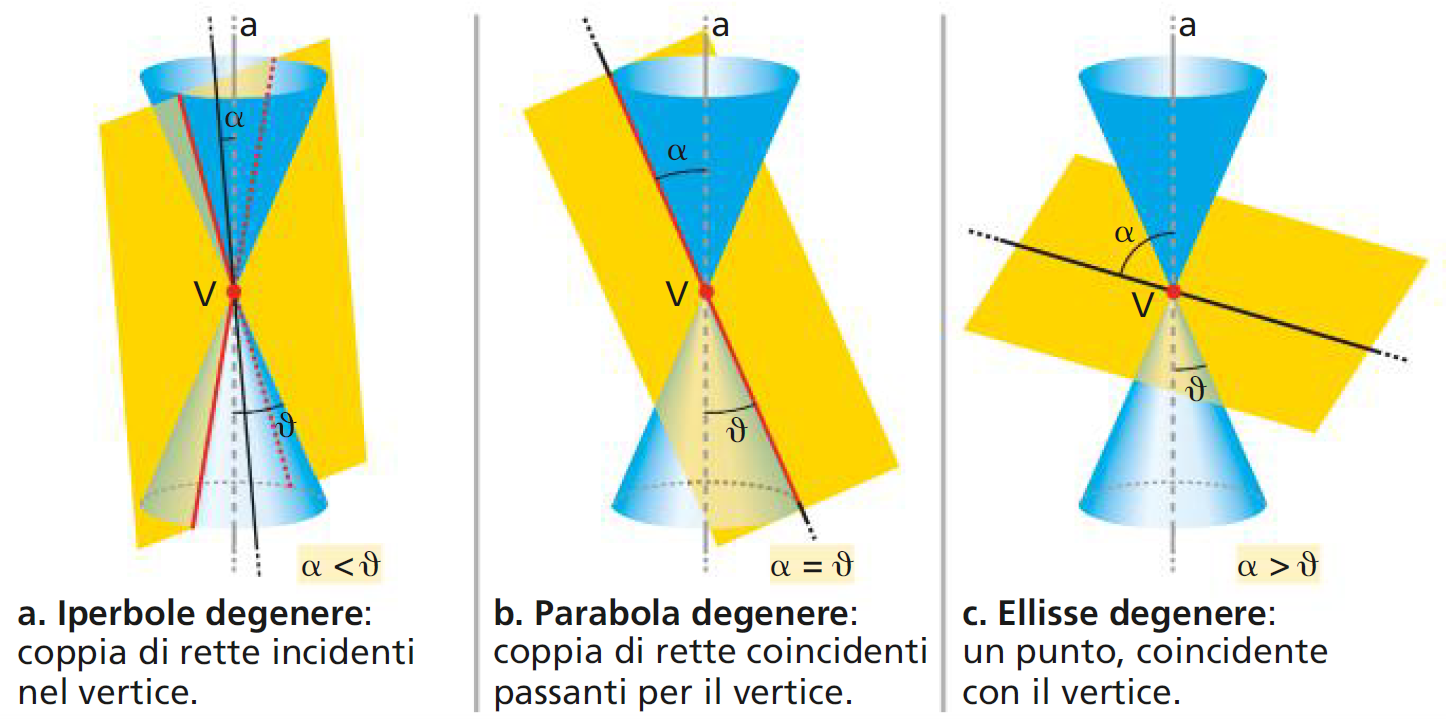
Se il piano che interseca la superficie conica passa per il vertice, al variare dell’angolo \( \alpha \) si ottengono le coniche degeneri della figura qui sotto:

Fai variare l'angolo di rotazione per ottenere le coniche descritte.